Blocked rotor test
A blocked rotor test is conducted on an induction motor. It is also known as short circuit test, locked rotor test or stalled torque test.[1] From this test, short circuit current at normal voltage, power factor on short circuit, total leakage reactance, and starting torque of the motor can be found.[2][3] The test is conducted at low voltage because if the applied voltage was normal voltage then the current through the stator windings would be high enough to overheat the windings and damage them.[4] The blocked rotor torque test is not performed on wound-rotor motors because the starting torque can be varied as desired. However, a blocked rotor current test is conducted on squirrel cage rotor motors.[5]
Contents
Method[edit]
In the blocked rotor test, the rotor is locked.[6] A low voltage is applied on the stator terminals so that there is full load current in the stator winding, and the current, voltage and power input are measured at that point. When the rotor is stationary, the slip,  .[7] The test is conducted at
.[7] The test is conducted at  the rated frequency as recommended by IEEE, because the rotor's effective resistance at low frequency may differ at high frequency.[8][9] The test can be repeated for different values of voltage to ensure the values obtained are consistent. As the current through the stator may exceed the rated current, the test should be conducted quickly.[10] By using the parameters found by this test, the motor circle diagram can be constructed.[11]
the rated frequency as recommended by IEEE, because the rotor's effective resistance at low frequency may differ at high frequency.[8][9] The test can be repeated for different values of voltage to ensure the values obtained are consistent. As the current through the stator may exceed the rated current, the test should be conducted quickly.[10] By using the parameters found by this test, the motor circle diagram can be constructed.[11]
Calculations involved[edit]
Short circuit current at normal voltage[edit]
 is the short circuit current at voltage
is the short circuit current at voltage 
 is the short circuit current at normal voltage
is the short circuit current at normal voltage 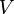

Short circuit power factor[edit]
 is the total input power on short circuit
is the total input power on short circuit
 is the line voltage on short circuit
is the line voltage on short circuit
 is the line current on short circuit
is the line current on short circuit
 is the short circuit power factor
is the short circuit power factor
 [12]
[12]
Leakage reactance[edit]
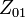 is the short circuit impedance as referred to stator
is the short circuit impedance as referred to stator
 is the leakage reactance per phase as referred to stator
is the leakage reactance per phase as referred to stator

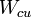 is the total copper loss
is the total copper loss
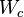 is the core loss
is the core loss
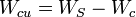



See also[edit]
References[edit]
- ^ "Motor testing methods". Electronic Systems of Wisconsin, Inc.
- ^ "Blocked rotor test". Sakshat virtual labs.
- ^ de Swardt, Henk. "The Locked rotor test explained" (PDF). Marthinusen & Coutts (Pty.) Ltd.
- ^ "Motor testing methods". Electronic Systems of Wisconsin, Inc.
- ^ Industrial Power Engineering and Applications Handbook. Newnes.
- ^ "Blocked rotor test". Sakshat virtual labs.
- ^ B.L. Theraja, A.K. Theraja (2010). Electrical Technology volume 2 (Twenty third revised multicolour ed.). S. Chand. p. 1317. ISBN 81-219-2437-5.
- ^ Knight, Dr Andy. "Electrical Machines". Department of Electrical and Computer engineering, University of Alberta.
- ^ Pitis, CD. "femco squirrel.doc". Femco mining motors.
- ^ "Motor testing methods". Electronic Systems of Wisconsin, Inc.
- ^ Deshpande, M.V. Electrical Machines. PHI Learning Pvt. Ltd.
- ^ Deshpande, M.V. Electrical Machines. PHI Learning Pvt. Ltd.